Example pages containing: tips | resources | functions/procedures
The fourier_info, ezfftf and ezfftb can be used to perform variations of Fourier Analysis. Using these functions on a variable with longitude as the rightmost dimension performs spatial analysis. To examine temporal harmonics, the input series must be reordered so the dimension 'time' is the rightmost dimension.
fanal_1.ncl:
A variable (here, gropotential height at 500 hPa) dimensioned (time,lat,lon)
is examined to determine the amplitude, phase (1st maximum) and percent variance explained. Harmonics 1 and 2 are displayed.
fanal_2.ncl:
Two similar variables TREFHT (temperature at 2m) and TSKIN (temperature
at actual surface) are compared via harmonic analysis.
fanal_3.ncl:
A forward fast Fourier transform (ezfftf) performs
a 'Fourier Analysis'. Selected coefficents are set to zero to isolate
different waves. A backward fast Fourier transform (ezfftb)
is used to perform a 'Fourier Synthesis'.
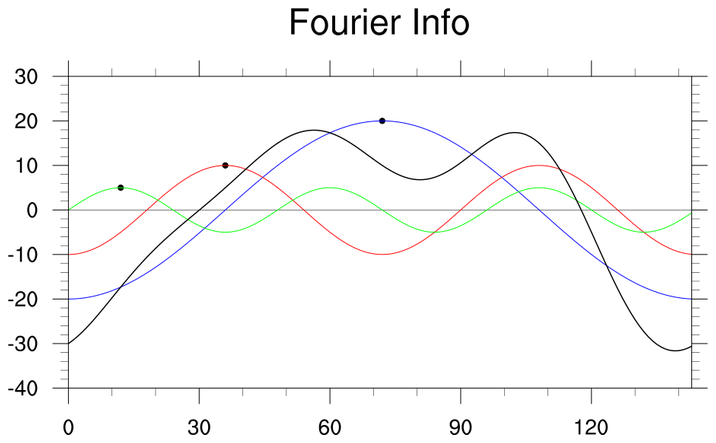
fanal_4.ncl:
Create three simple sine waves (blue, red, green) and combine the waves
(superposition; black).
Use fourier_info on the combined series
to derive the amplitudes, phases and per-cent
variances explained by each harmonic. Use a polymarker to mark the
derived locations of the harmonic phase. The (edited) printed output is:
Variable: finfo
Type: float
Total Size: 36 bytes
9 values
Number of Dimensions: 2
Dimensions and sizes: [3] x [3] ; [3] x [nhx]
Coordinates:
(0,0) 20 <=== Amplitudes
(0,1) 10
(0,2) 5
(1,0) 72 <=== Phases: location of first maximum
(1,1) 36
(1,2) 12
(2,0) 76.19048 <=== % variance
(2,1) 19.04762
(2,2) 4.761904
fanal_5.ncl:
Similar to fanal_3 and fanal_4 except that spherical
harmonic analysis and synthesis are also used.