WARNING
Is your data on a native grid? A native grid is a model that was
designed from the beginning with a particular map projection. In order
to plot the data exactly as the designers planned, we do not want to
transform the data to a projection, but simply plot it. This is the
essence of the examples on this page.
Just because your data has 2D lat/lon arrays, does not make it a
native grid. Native grids are plotted differently than other data
with 2D coordinates.
In all cases, you MUST use the
mpLimitMode="Corners" method to specify the grid. Other methods will
result in an incorrect mismatch between the data and the map.
Additionally, you must set
tfDoNDCOverlay = True so that the data is not transformed to the
projection, but is simply placed there since it is already on a
projection.
pmTickMarkDisplayMode = "Always" turns on the automatic tickmarks
(available since NCL version 4.2.0.a023).
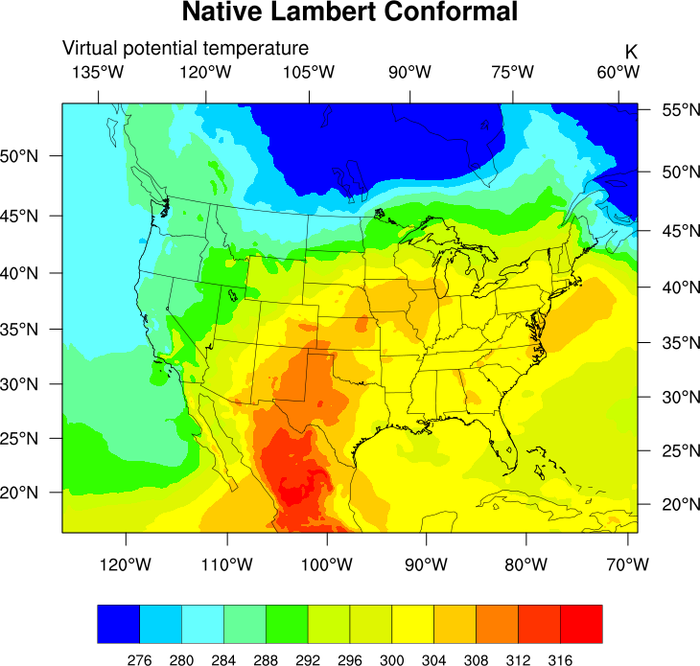
lcnative_1.ncl: An example of a
netCDF Lambert Conformal native grid. netCDF files may or
may not contain the parallel information needed to plot the grid
correctly. Grids on GRIB files (see example 4) contain this
information.
mpProjection = "LambertConformal", sets the projection.
The three pieces of information that are required for this projection
(with example values) are:
mpLambertParallel1F = 30.
mpLambertParallel2F = 55.
mpLambertMeridianF = 45.
The problem with Lambert grids is they are are sometimes described
by a meridian, parallel and a delta X and delta Y in meters at the
intersection of the meridian and top parallel. It can be VERY
difficult to come up with corner points when this method is used.
A note about this particular example: Since no information was able
on the grid, we assumed that the lat, lon arrays started in the lower
left corner. Another RCM-2 user found a different array order, which
resulted in the following "corners" selections:
mpLeftCornerLatF = lat2d(nlat-1,0)
mpLeftCornerLonF = lon2d(nlat-1,0)
mpRightCornerLatF = lat2d(0,nlon-1)
mpRightCornerLonF = lon2d(0,nlon-1)
