NCL Home> Application examples> Models || Data files for examples

ORCA Grid

Non-uniform grids and triangular mesh conversion

The ORCA grid used in the examples on this page is a non-uniform grid. It was given to us by Christophe Cassou from the Centre National de la Recherche Scientifique (CNRS/CERFACS) in Toulouse. This grid is common in Europe, particularly in France; the IPSL centre ("Institut Pierre-Simon Laplace model") developed it. More information on the grid can be obtained here.

It is better to convert this grid to a triangular mesh (available since NCL version 4.2.0.a032) rather than interpolate it to a uniform grid before contouring. Note that only contouring is available with triangular mesh conversion at this time.

If the input array to a gsn_csm graphical interface is one- dimensional, and also has one-dimensional lat/lon arrays of the same length, NCL automatically uses triangular mesh conversion. The lat/lon information must be provided by setting sfXArray and sfYArray.

For more information on non-uniform grids that NCL can handle, see the document "Non-uniform grids that NCL can contour."

orca_1.ncl: Note that the trGridType resource is set to "TriangularMesh" in this example, so that it will use a triangulation algorithm to contour the mesh.

The lat/lon information must be provided by setting the resources sfXArray and sfYArray.

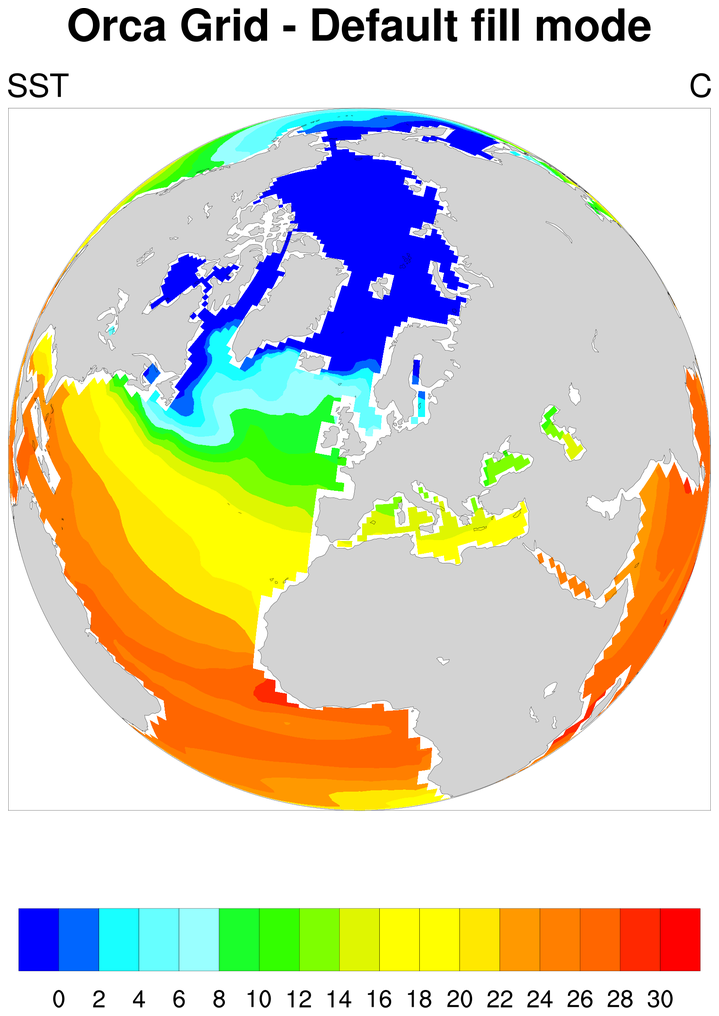
This example compares the results between the default cnFillMode value of "AreaFill" and "RasterFill".

orca_2.ncl: This example is very similar to the previous example, except that it shows what happens when you set cnFillMode value of "CellFill", and then how to turn on the cell edges and missing value cell edges with the resources cnCellFillEdgeColor and cnCellFillMissingValEdgeColor.

ORCA Grid

Non-uniform grids and triangular mesh conversion

NCL is a product of the Computational & Information Systems Laboratory at the National Center for Atmospheric Research (NCAR) Contact webmaster

NCL is a product of the Computational & Information Systems Laboratory at the National Center for Atmospheric Research (NCAR)
Contact webmaster