NCL Home > Documentation > Functions > Empirical orthogonal functions

eofunc_north

Use North et al (MWR, 1982) equation 24 to evaluate eigenvalue separation.

Available in version 6.3.0 and later.

Prototype

load "$NCARG_ROOT/lib/ncarg/nclscripts/csm/contributed.ncl"  ; This library is automatically loaded
                                                             ; from NCL V6.2.0 onward.
                                                             ; No need for user to explicitly load.

	function eofunc_north (
		eval   [*] : numeric,          
		N      [1] : integer or long,  
		prinfo [1] : logical           
	)

Arguments

eval

Eigenvalues to be tested. These are returned as attributes of the EOFs returned by eofunc or eofunc_Wrap: specifically, eval. Actually, any of the following attributes could probably be used: pcvar, eval_transpose or eval. Using pcvar is probably the clearest if prinfo=True.

Maximum possible number of eigenvalues. Typically, in climate applications, this is the number time steps.

prinfo

Print the calculated 'delta lambda', the eigenvalues, the lower and upper test bounds and the 'separated significance' (sig).

Return value

A one dimensional logical array containing True or False. This indicates if eigenvalues are significantly separated.

Description

Uses North et al equation 24 to see if eigenvalues are significantly separated.


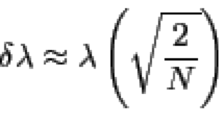
 North, G.R. et al (1982): Sampling Errors in the Estimation of Empirical Orthogonal Functions.
 Mon. Wea. Rev., 110, 699-706.
 doi:    http://dx.doi.org/10.1175/1520-0493(1982)110<0699:SEITEO>2.0.CO;2

Examples

See: Applications Example 6

Example 1


   f      = addfile("erai_1989-2009.mon.msl_psl.nc","r") 
   p      = f->SLP(::12,{0:90},:)                      ; p(time,latitude,longtitude)
   printVarSummary(p)                                  ; p(21,61,240)
   
   w      = sqrt(cos(0.01745329*p&latitude)            ; weights(61)
   wp     = p*conform(p, w, 1)                        ; wp(21,61,240)
   copy_VarCoords(p, wp)                             ; wp(time,lat,lon)
   printVarSummary(wp)   ; [time | 21] x [latitude | 61] x [longitude | 240]
   
   x      = wp(latitude|:,longitude|:,time|:)          ; reorder data
   neof   = 4
   eof    = eofunc_Wrap(x, neof, False)
   eof_ts = eofunc_ts_Wrap
   
   printVarSummary(eof) 
   printVarSummary(eof_ts) 
   
   ;*******************************************
   ; North significance test: Note any of the following could be used
   ;*******************************************
   dimp   = dimsizes(p)
   ntim   = dimp(0)
   
   prinfo = True
   sig_ev  = eofunc_north(eof@eval, ntim, prinfo)

   sig_pcv = eofunc_north(eof@pcvar, ntim, prinfo)
   sig_evt = eofunc_north(eof@eval_transform, ntim, prinfo)

The (edited) output