NCL Home> Application examples> Data Analysis || Data files for some examples

Example pages containing: tips | resources | functions/procedures

NCL: Bootstrapping and Resampling

Bootstrapping is a statistical method that uses data resampling with replacement (see: generate_sample_indices) to estimate the robust properties of nearly any statistic. Most commonly, these include standard errors and confidence intervals of a population parameter like a mean, median, correlation coefficient or regression coefficient. Bootstrapping statistics has two attractive attributes:

  • It is particularly useful when dealing with small sample sizes.
  • It makes no apriori assumption about the distribution of the sample data.

References: 

Computer Intensive Methods in Statistics 
   P. Diaconis and B. Efron 
   Scientific American (1983), 248:116-130  
   doi:10.1038/scientificamerican0583-116
   http://www.nature.com/scientificamerican/journal/v248/n5/pdf/scientificamerican0583-116.pdf
   
An Introduction to the Bootstrap 
   B. Efron and R.J. Tibshirani, Chapman and Hall (1993) 

Statistical methods for the analysis of simulated and observed climate data
   Barbara Hennemuth et al (2013)
   Applied in projects and institutions dealing with climate change impact and adaptation
    CSC Report 13
   
Bootstrap Methods and Permutation Tests: Companion Chapter 18 to the Practice of Business Statistics
   Hesterberg, T. et al (2003)
   http://statweb.stanford.edu/~tibs/stat315a/Supplements/bootstrap.pdf

Climate Time Series Analysis: Classical Statistical and Bootstrap Methods
   M. Mudelsee (2014) Second edition. Springer, Cham Heidelberg New York Dordrecht London
   ISBN: 978-3-319-04449-1, e-ISBN: 978-3-319-04450-7
   doi: 10.1007/978-3-319-04450-7
   xxxii + 454 pp; Atmospheric and Oceanographic Sciences Library, Vol. 51

NCL (6.4.0 ) currently has four bootstrap statistic functions and one bootstrap utility function:

Some NCL bootstrap functions allow for subsampling (n<N) and for sequential blocks (sequences) of values. More involved sampling strategies may require custom codes. A user could extract one of the above core functions from the contributed.ncl library and modify as needed.
Several of the NCL examples use two 'law school' data sets from Efron and Tibshirani (1993). These contain LSAT (Law School Admission Test) scores and subsequent GPAs (Grade Point Averages). One data set, law_school_82.txt, contains the LSAT and GPA for 82 law schools; the second data set, law_school_15.txt contains a random sample from 15 of the 82 schools. The reason for using these is that WWW-accessible results using both R and Matlab_1 and Matlab_2 are readily available for comparison purposes. See: regression Example 7 for a visualization of these files.

resampling_1.ncl: These distributions of sampling indices illustrate properties of resampling with replacement from a uniform distribution using generate_sample_indices. Clearly, a reasonably large N is needed to 'reasonably' sample all combinations.

A simple example of using sampling with replacement to derive a bootstrapped mean and 95% confidence limits. Here x(N): 

   nBoot =   10000                           
   xBoot = new (nBoot, typeof(x))
   
   do ns=0,nBoot-1                        ; generate multiple estimates
      iw = generate_sample_indices(N,1)) ; indices with replacement
      xBoot(ns) = dim_avg_n( x(iw), 0 )  ; compute average 
   end do
   
   xAvgBoot = dim_avg_n(xBoot,0)         ; Averages of bootstrapped samples
   xStdBoot = dim_stddev_n(xBoot,0)      ; Std Dev  "        "        "
   xStdErrBoot = xStdBoot/nBoot           ; Std. Error of bootstrapped estimates
   
   ia = dim_pqsort_n(xBoot, 2, 0)        ; sort bootstrap means into ascending order
   
   n025     = round(0.025*(nBoot-1),3)    ; indices for sorted array
   n500     = round(0.500*(nBoot-1),3)                             
   n975     = round(0.975*(nBoot-1),3)
   
   xBoot_025= xBoot(n025)                 ;  2.5% level
   xBoot_500= xBoot(n500)                 ; 50.0% level  (median)
   xBoot_975= xBoot(n975)                 ; 97.5% level

Note: since 'x(N)' is rank one, the following functions could have been used in place of the dim_*_n functions: avg, stddev and qsort. Of course, the arguments would have to change accordingly.

bootstrap_stat_1.ncl: These illustrate various properties of the mean (opt@stat=0) using different bootstrap sampling parameters.

  • use the 82-school data set and resample using the full data set (N=82, n=82)
  • use the 82-school data set and resample using 15-member subsets (N=82, n=15)
  • use the 15-school data set and resample using only this subset (N=15, n=15)
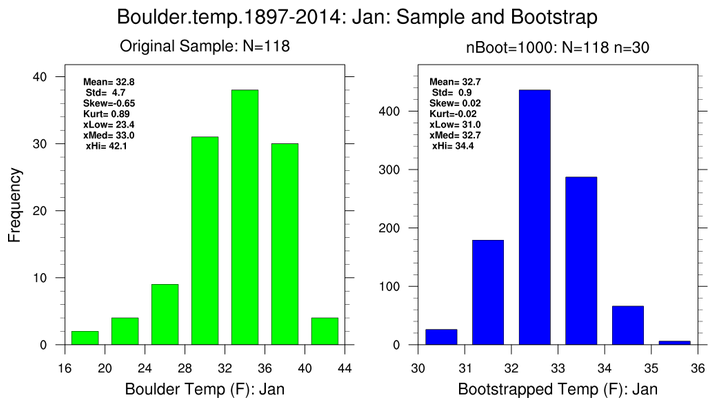
In all cases, the bootstrapped estimates are generated using nBoot=1000. Each figure contains two histograms. The left (green) histogram show the distribution of the original sample and assorted 'conventional' statistics: sample mean, standard deviation, standard error, t-value and the 2.5% and 97.5% confidence bounds . The right (blue) histogram shows the distribution of bootstrapped sample means; the standard deviation of the bootstrapped means; the standard error of the bootstrapped means and the 2.5% and 97.5% bootstrapped values.
bootstrap_stat_1a.ncl: This is the same as bootstrap_stat_1.ncl except the figure includes graphical markers (here, all asterisks) that indicate the location of the bootstrapped low (2.5%), median (50%) and high (97.5%) values. The procedure which attaches the markers to the histogram graphical object is named histogram_marker.ncl .
bootstrap_stat_2.ncl: Bootstrap January monthly mean temperatures (degF; left histogram pair) and May monthly precipitation totals (inches) totals (right histogram pair) for Boulder, CO for the period 1897-2014. Estimate various properties of the mean. The total sample size for each month is N=114. Here, 30-year sub-samples (n=30) are are generated nBoot=1000 times.
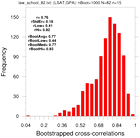bootstrap_correl_1.ncl: These estimate the correlation coefficient between the 82-school LSAT and GPA using classical statistics and via the bootstrap method.

The first rule of data processing is look at your data; the second rule of data processing is understand your data. This example illustrates two simple approaches.

  • a simple line plot of the 82-school LSAT and GPA values
  • histograms of each variable
  • use the 82-school data set and resample using the full data set (N=82, n=82)
  • use the 82-school data set and resample using 15-member subsets (N=82, n=15)

The two text boxes show values derived using the original single sample the bootstrap estimates. The latter have used the Fischer z-transform to calculate various statistics.

bootstrap_correl_1.ncl: This example estimates the correlation coefficient between the 15-school LSAT and GPA using classical statistics and via the bootstrap method.

This example follows the methodology of the previous example.

  • a simple line plot of the 15-school LSAT and GPA values
  • histograms of each variable
  • Since N=15, only n=15 is used.

This example (N=15, n=15) 'matches' the Matlab_1 example.

The two text boxes show values derived using the original single sample the bootstrap estimates. The latter have used the Fischer z-transform to calculate various statistics.

bootstrap_correl_2.ncl:

Correlate the SOI_SIGNAL (Southern Oscillation Index Signal) and monthly temperature anomalies. Show the 2.5% and 97.5% limits derived using 'conventional' (left column) and bootstrap (right column) statistics.

Reference: Trenberth (1984), "Signal versus Noise in the Southern Oscillation" Monthly Weather Review 112:326-332

bootstrap_regcoef_1.ncl: These estimate the linear regression coefficient between the LSAT and GPA. Additional information based upon the original sample is provided via regline_stats.
  • use the 82-school data set and resample using the full data set (N=82, n=82)
  • use the 82-school data set and resample using 15-member subsets (N=82, n=15)
  • use the 15-school data set and resample using only this subset (N=15, n=15)
bootstrap_regcoef_2.ncl: Use the UKMO global annual temperature anomalies to estimate the linear regression coefficient (trend=degC/year).

  • use the N=165 annual values with no sub-sampling (n=N=165); left histogram
  • use the N=165 annual values with sub-sampling n=30 year; right histogram

See also: manken_1.ncl.

bootstrap_regcoef_3.ncl: Read annual temperature values spanning 1500 years (600-2099) from the Large ENSemble (LENS) control run. Plot the time series with the fitted regresions line; the variable distribution and the regression coefficient distributions derived using a 36-year sub-sampling period: (i) default random sampling; (ii) opt="sequential", and (iii) methodical (overlapping) segments (running blocks). Technically, (iii) is not bootstrapping because there is no random sampling. The point is that (ii) and (iii) are essentially identical. Hence, no explicit 'running_block' or 'running_sequential' option is offered.

Why the difference in regression coefficient magnitudes between the default (i) and the sequential (ii) and running blocks (iii). The reason is that the default random sampling is using n=36 values from the entire 1500 year series. The (ii) opt="sequential" and (iii) running-block were sample n=36 sequential values. The sequential values have some 'memory.'

bootstrap_diff_1.ncl:

Calculate the conventional and bootstrapped difference statistics between two samples using default sampling sizes: NX=25 and NY=18. (See the left figure.) The bootstrapped confidence intervals 'match' the R-generated 95% confidence values of 2.14 (2.5%) and 6.77 (97.5%). The conventional confidence limits provided by the reference are 1.96 and 6.80. NCL's and R's p-value=0.0007474 match.

The right figure shows the distribution with user specified sub-sampling: specifically: opt=True with opt@sample_size_x=9 and opt@sample_size_y=7.

bootstrap_diff_2.ncl:

Using Boulder, CO annual precipitation calculate the conventional and bootstrapped difference statistics between two periods: (a) 1897-1979 and (b) 1980-2014.